Крутильные колебания – это вращательное движение тела, подвешенного на упругой нити (стальной проволоке), вокруг вертикальной оси, выражающееся в его попеременном отклонении в ту и другую сторону от положения равновесия. Силовая величина, характеризующая динамику такого движения, является следствием деформации нити. Деформация – это изменение формы и размеров тела под действием приложенных к нему сил. Если после прекращения действия силы тело принимает первоначальные размеры и форму, то деформация называется упругой. Существует несколько видов деформации тел: растяжение, сжатие,
кручение, сдвиг, изгиб. При этом внутри деформированного тела возникает противодействующая сила, равная по величине деформирующей силе и называемая упругой силой. Величина упругой силы F упр . , возникающей при малых деформациях любого вида, прямо пропорциональна величине деформации x , то есть изменению размеров тела, что в общем виде выражается соотношением:
F упр. = – kх (10)
где k – коэффициент пропорциональности, называемый коэффициентом упругости. Соотношение (10) называется законом Гука. Знак минус указывает на противоположные направления упругой силы и величины деформации.
При закручивании нити с подвешенным телом на некоторый угол φ (рис. 1) возникающее в нити противодействие представляет собой момент силы М , значение модуля которого пропорционально углу φ, а направление, как и при любой деформации, противоположно ей, т.е. углу закручивания:
М = – D φ (11)
Здесь:D – модуль кручения (коэффициент упругости), характеризующий упругие свойства нити.
Для вращательного движения тела второй закон Ньютона записывается в виде:
М = J ε (12)
где J – момент инерции тела, ε = d 2 φ/dt 2 – угловое ускорение, М – суммарный момент сил, в данном случае представляющий собой момент упругой силы, которая возникает при закручивании упругой нити (проволоки) на угол φ. Подставляя в это уравнение выражение для момента упругой силы (11), мы получим линейное дифференциальное уравнение второго порядка, описывающее движение тела при крутильных колебаниях:
J (d 2 φ/ dt 2 ) + D φ = 0 (13)
Решение этого уравнения имеет вид:
φ = φ 0 sin (ω t + φ o ) (14)
где φ – угол поворота тела в момент времени t , φ 0 – максимальный угол поворота тела при колебаниях (амплитуда колебаний), φ o – начальная фаза колебаний, а коэффициент при t , составляющий ω = (D / J ) 1/2 , – циклическая (или круговая) частота колебаний. Поскольку, с другой стороны,
циклическая частота колебаний, по определению, равна 2π/T (T – период колебаний), то можно записать равенство:
ω = (D / J ) 1/2 = 2π/ T (15)
откуда следует уравнение, связывающее период крутильных колебаний с моментом инерции тела, подвешенного на упругой нити, и модулем кручения нити:
T = 2π(J / D ) 1/2 (16)
Описание установки и метода измерений:
Для определения моментов инерции твердых тел в работе используется установка, показанная на рис. 2.

На основании 1 расположен электронный блок 2 с миллисекундомером и счетчиком полных колебаний, а также укреплена колонка 3 , на которой находятся три кронштейна 4 , 5 , 6 . Кронштейны 4 и 6 имеют зажимы для подвеса рамки на упругих стальных нитях 7 . Рамка представляет собой две балки 8 , соединенных стержнями 9 . На стержнях с помощью цанговых зажимов 10 закрепляется в нужном положении подвижная балка 11 ,
которая позволяет (путем закручивания винта 12 ) укреплять в рамке исследуемые тела 13 , значительно отличающиеся по внешним размерам. На стальной плите, прикрепленной к кронштейну 5 , располагаются соединенные с электронный блоком электромагнит 14 и фотоэлектрический датчик 15 , а также угловая шкала (на рисунке не показана), которая служит для задания амплитудного значения угла закручивания.
Работа на установке проводится в следующем порядке:
Закрепить электромагнит в положении, которое соответствует определенному углу закручивания рамки (задается преподавателем).
Если требуется заданием, укрепить в рамке исследуемое тело. Для этого:
а) ослабить зажимы 10 ;
б) передвигая подвижную балку 11 , зажать тело между коническим выступом нижней балки и конусом винта 12 , затянуть зажимы 10 ;
в) окончательно укрепить тело, закручивая винт 12 .
Включить питающее напряжение нажатием клавиши "Сеть". При этом должны светиться лампочки фотоэлектрического датчика и индикатора секундомера.
Нажать клавишу "Сброс" для обнуления индикатора секундомера, генерирования сигнала разрешения на измерение и включения обмотки электромагнита.
Повернуть рамку прибора так, чтобы в отклоненном состоянии она была зафиксирована электромагнитом.
Нажать клавишу "Пуск". Нажатие этой клавиши запускает секундомер и отключает электромагнит. Рамка при этом отпускается и начинает совершать крутильные колебания, которые подсчитываются в электронном блоке посредством сигналов, поступающих от фотоэлектрического датчика 15 .
После совершения рамкой определенного числа колебаний систему остановить нажатием кнопки "Стоп". Индикаторы электронного блока указывают число N совершенных колебаний и общее время t , за которое они были совершены.
Задание 1. Определение модуля кручения.
При использовании установки крутильных колебаний для определения моментов инерции твердых тел необходимо знать величину модуля кручения D нитей подвеса 7 рамки. Поскольку упругие свойства
материала при кручении зависят от многих факторов, то значение модуля D определяют экспериментально. В настоящей работе используется динамический метод измерения модуля кручения, основанный на зависимости периода Т крутильных колебаний рамки, подвешенного на проволоке, от упругих свойств материала проволоки.
Согласно уравнению (16), период колебаний Т зависит как от модуля кручения D , так и от момента инерции J системы, совершающей колебания. Поэтому измерения проводят с помощью эталонных тел, моменты инерции которых J т известны, или легко рассчитываются. Система, совершающая колебания, включает в себя эталонное тело и рамку, моментом инерции J р которой нельзя пренебречь. Так как эталонное тело и рамка совершают вращательное движение вокруг одной и той же оси, то, согласно уравнению (9), их моменты инерции суммируются:
J = J р + J т (17)
Если выразить момент инерции из уравнения (16), то:
J = J р + J т = Т 2 D /(4 2 ) (18)
Поскольку момент инерции рамки J р неизвестен, измерения проводят в два этапа, используя два различных эталонных тела с моментами инерции J т1 и J т2 . В этом случае мы имеем систему двух уравнений:
J р + J т1 = Т 1 2 D /(4 2 ) (19а)
J р + J т2 = Т 2 2 D /(4 2 ) (19б)
Вычитая одно из другого, получаем выражение для модуля кручения, не содержащее неизвестных (или не определяемых в эксперименте) параметров:
D = 4 2 (J т1 – J т2 )/(Т 1 2 – Т 2 2 ) (20)
Измерения проводятся следующим образом:
Взять первое эталонное тело – один из двух дисков. Измерить штангенциркулем его толщину l и диаметр. Получить значение радиуса диска r . Взвесить диск на технических весах, или принять известное
значение его массы m (может быть указано на диске или на установке). По формуле (4) рассчитать момент инерции диска J т1 и занести это значение в таблицу 1.
Провести операции согласно пунктам 1-7 порядка работы на установке (см. раздел «Описание установки и метода измерений»). Полученные значения N и t для первого тела занести в таблицу 1.
Еще два раза определить N и t (операции по пунктам 4-7 порядка работы на установке) и занести их в те же колонки.
Повторить предыдущие операции (1-4) для другого диска, занося значения J т2 , N , t , T 2 и T 2ср в таблицу 1 ("Второе тело").
Используя полученные значения J т1 , J т2 , Т 1 и Т 2 , по формуле (20) рассчитать и занести в таблицу 1 значение модуля кручения D .
Методом косвенных измерений найти абсолютную и относительную погрешности измерений.
Таблица 1.
|
Первое тело |
Второе тело |
D , Нм |
|||||||||
|
J т1 , кг·м 2 |
T 1 , с |
T 1ср, с |
J т2 , кг·м 2 |
t , с |
T 2 , с |
T 2ср, с |
|||||
Задание 2. Определение момента инерции пустой рамки.
Освободить рамку от дополнительных тел и три раза определить значения N и t для пустой рамки (аналогично тому, как это делалось в предыдущем задании для рамки с телом) и занести их в таблицу 2.
Определить три значения периода колебаний пустой рамки T 0 , рассчитать их среднее значение T 0ср и занести эти данные в таблицу 2.
Тремя способами определить значение момента инерции пустой рамки:
а) используя полученное значение периода колебаний T 0ср и значение D из таблицы 1, рассчитать J р0 по формуле, аналогичной формуле (18):
J р0 = (Т 0ср ) 2 D /(4 2 )
б) используя значения J т1 , Т 1 и D из таблицы 1, рассчитать J р1 по формуле, полученной из формулы (19а):
J р1 = Т 1 2 D /(4 2 ) – J т1
в) используя значения J т2 , Т 2 и D из таблицы 1, рассчитать J р2 по формуле, полученной из формулы (19б):
J р2 = Т 2 2 D /(4 2 ) – J т2
Сравнить полученные значения J р0 , J р1 и J р2 ; рассчитать из них среднее значение момента инерции пустой рамки J р-ср и занести его в таблицу 2.
Вычислить абсолютную и относительную погрешности.
Таблица 2.
|
N |
t , с |
T 0 , с |
T 0ср , с |
J р0 , кг·м 2 |
J р1 , кг·м 2 |
J р2 , кг·м 2 |
J р-ср , кг·м 2 |
|
Задание 3. Определение момента инерции тела.
Закрепить исследуемое тело – прямоугольный параллелепипед – в рамке, совместив с осью вращения одну из главных осей инерции данного тела. Три раза определить N и t (так же, как это делалось в предыдущих заданиях) и занести эти значения, а также соответствующие им значения T = t /N , для оси № I в таблицу 3.
Повторить проделанные операции для двух других главных осей инерции исследуемого тела. Полученные значения N , t и T для оси № II и для оси № III занести в таблицу 3.
Для всех трех осей из трех значений периода колебаний рамки с телом T рассчитать их средние значения T ср и занести эти данные в таблицу 3.
Используя полученное ранее среднее значение момента инерции рамки Ј р‑ср (таблица 2), из соотношения Ј т = Ј – Ј р‑ср определить значения моментов инерции тела Ј т относительно трех его главных осей инерции и занести эти значения в таблицу 3.
Таблица 3.
|
T ср, с |
J , кг·м 2 |
J т, кг·м 2 |
|||||
Контрольные вопросы для подготовки к работе:
Какая величина называется моментом инерции материальной точки и твердого тела?
По какому закону происходят крутильные колебания?
Что такое модуль кручения и от чего он зависит?
Какие величины измеряют в данной работе, какие вычисляются и по каким формулам?
Контрольные вопросы для защиты работы:
Что такое момент инерции и каков физический смысл этой величины?
Каковы единицы измерения момента инерции?
Что называется упругой деформацией?
Вывести формулу для определения модуля кручения.
Какова природа крутильных колебаний и по какому закону они происходят?
Что называется моментом импульса тела? Как он направлен?
В чем состоит теорема Штейнера?
Написать формулу периода крутильных колебаний.
УЧЕБНОЕ ИЗДАНИЕ
Макаров Игорь Евгеньевич, д.х.н. профессор
Юрик Тамара Константиновна, к.х.н. доцент
Гл. 7.
Крутильные колебания
Рис. 7.14. Одно-, двух- и трехмассовые крутильные системы
Введение . В дизельной установке крутильные колебания испытывают коленчатый вал, промежуточные и гребной валы с навешенными на них массами (детали механизма движения отдельных цилиндров, маховик, соединительные муфты, гребной винт), связанные в единую упругую систему валопровода.
Крутильные колебания представляют собой периодические колебания в плоскости вращения навешенных на вал масс, при которых участки вала между массами скручиваются и раскручиваются под действием циклически меняющегося крутящего момента.
Любая конструкция под действием переменных сил испытывает два вида колебаний - свободные и вынужденные.
Свободные колебания . Эти колебания рассмотрим на примере простейшей крутильной системы, состоящей из вала длиной L, жестко закрепленного одним концом, и массы в виде диска 1, центр тяжести которого лежит на оси вала (рис.7. 14,а). Если к массе приложить момент М кр , то вал окажется скрученным (в пределах упругих деформаций) на угол +φ. В скрученном валу возникнет момент от сил упругости материала вала M y . Допустим теперь, что действие момента М Кр мгновенно прекратится. Под действием момента М у система будет возвращаться в исходное положение, однако вследствие инерции массы 1 она не остановится в положении равновесия и вал вновь окажется скрученным, но уже в обратном направлении (на угол - φ). Упругость вала снова вызовет поворот массы, и она по инерции перейдет через положение равновесия, т. е. процесс повторится.
Таким образом, после прекращения действия внешнего момента система будет совершать свободные колебания только за счет сил упругости материала вала и силы инерции массы. При этом вал будет скручиваться то в одном, то в другом направлениях. Принципиально ничего не изменится, если жесткое закрепление свободного конца вала заменить значительным сопротивлением колебаниям (например, насадить на вал гребной винт или маховик генератора) и, если во время совершения колебаний вал одновременно будет равномерно вращаться. При отсутствии сопротивлений свободные колебания могли бы продолжаться бесконечно долго с неизменными амплитудой и частотой.
Амплитуда колебаний (угол скручивания вала)
![]() (7.23)
(7.23)
где М кр - крутящий момент,
l - длина вала,
G - модуль упругости материала вала,
I р - полярный момент инерции сечения вала,
с - крутильная жесткость вала,
е - податливость вала.
Частота колебаний (число циклов колебаний в секунду)
(7.24)
где θ - момент инерции массы относительно оси вала. Рассмотренная простейшая крутильная система является одномассовой. Закрепив на свободном конце вала еще одну массу в виде диска (рис. 7.14,6), получим двухмассовую крутильную систему.
Если к массам 1 и 2 приложить моменты М кр и М с противоположных знаков, а затем мгновенно их снять, то при упругом колебании такой системы некоторое сечение вала (УУ) будет оставаться в покое, т. е. угловая амплитуда (угол скручивания φ) будет равна нулю. Это сечение вала называется узлом колебаний . Если отложить на диаграмме (см. рис.7.14) в соответствующем масштабе максимальные значения угловых амплитуд масс и соединить полученные точки прямой, то получим график угловых амплитудных отклонений масс от положения равновесия, иллюстрирующий форму колебаний. У двухмассовой системы форма колебаний имеет только один узел (точка У) и называется одноузловой.
В общем случае у многомассовой системы с i массами максимально возможное число форм колебаний равно i-1 . Действительная крутильная схема системы валопровода является сложной многомассовой системой, но при определении частоты свободных колебаний ее обычно упрощают и приводят к трехмассовой системе: двигатель-маховик-гребной винт (рис. 7.14, б). Такая система может иметь как одноузловую, так и двухузловую формы колебаний.
Каждая форма имеет свою частоту свободных колебаний, причем, чем выше форма колебаний (т. е. чем больше узлов), тем больше частота колебаний.
Вынужденные колебания. Эти колебания в системе валопровода возникают под действием периодически изменяющихся крутящих моментов от сил давления газов в цилиндрах и сил инерции поступательно движущихся масс. Указанные моменты называются возмущающими и, как известно, для одного цилиндра определяются выражениями:
![]()
![]()
Моменты М Г и Mj являются сложными периодическими функциями и в целях упрощения анализа могут быть разложены на элементарные составляющие - гармоники, изменяющиеся по закону синуса с различными амплитудами и частотами. Например, крутящий момент от сил давления газов можно представить в виде ряда
М г = М ср + M 1 + М 2 + М 3 + ... + М к +…, (7.25)
где М cр - средний крутящий момент одного цилиндра за цикл; М 1 , M 2 , М 3 ...,М к - текущие значения гармонических составляющих.
Подобным образом можно разложить в ряд крутящий момент от сил инерции поступательно движущихся масс. Такое разложение называется гармоническим анализом крутящего момента двигателя.
Каждая гармоника имеет свой порядок, который показывает число полных изменений гармоники за один оборот вала. Так как в четырехтактном двигателе рабочий цикл осуществляется за два оборота вала, а в двухтактном - за один, то 1, 2, 3 и к-и . члены выражения (7.25) будут являться гармониками в двигателях: двухтактных - 1, 2, 3, к-го порядка; четырехтактных -1/2, 1, 1 1/2, к/2-го порядка.
Каждая гармоника возбуждает в валу вынужденные колебания определенной частоты, пропорциональной порядку гармоники к и частоте вращения вала п, т. е. v в =кп кол/мин.
Наибольшие амплитуды колебаний вызывают гармоники, порядок которых равен или кратен числу вспышек в цилиндрах за один оборот вала двигателя (главные гармоники). Наименьший порядок главной гармоники к = i / т , где i - число цилиндров; т - коэффициент тактности двигателя. Остальные порядки главных гармоник будут кратны ему. Например, для шестицилиндрового четырехтактного двигателя к = 6/2 = 3 (кратные порядки: 6, 9, 12 и т. д.), для двухтактного двигателя к = 6/1 = 6 (кратные порядки: 12, 18, 24 и т. д.).
Таким, образом, вынужденные крутильные колебания под действием крутящего момента можно рассматривать как сумму гармонических колебаний под действием отдельных составляющих этого момента.
Средний крутящий момент М ср (постоянная составляющая полного момента) не вызывает крутильных колебаний и приводит валовую систему во вращение, создавая постоянное напряжение скручивания Т ср на участке валопровода между двигателем и гребным винтом.
Гармонические составляющие полного момента являются возмущающими моментами, вызывающими крутильные колебания, дополнительные знакопеременные напряжения σ доп , которые накладываются на постоянное напряжение от М cр , снижая прочность коленчатого вала и валопровода.
Резонанс, критическая частота вращения и запретные зоны
Совпадение частоты какой-либо формы свободных колебаний с частотой какой-либо гармонической составляющей возмущающего момента называется резонансом, а частота вращения, при которой наступает резонанс, называется критической (или резонансной) частотой.
Из равенства частот v c = v в = кп кол./с вытекает, что критическая частота вращения
C -1 (7.26)
При резонансе амплитуда крутильных колебаний (угол скручивания вала) и пропорциональные ей дополнительные напряжения кручения увеличиваются и могут оказаться опасными для прочности вала и вызвать его поломку (рис. 7.15, а, б). Опасные режимы работы можно определить с помощью графика (см. рис.7.15, б).
На рис. 7.15,
а
резонансные частоты появляются при пересечении линий собственных колебаний вала двигателя
v
c
1
и
v
c
2
с двумя гармоническими составляющими вынужденных колебаний
v
b
1
и
v
b
2
.
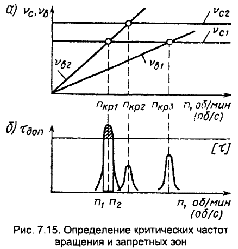
На этот же график наносится линия допускаемого напряжения от крутильных колебаний σ доп установленного из соображений усталостной прочности материала вала. Если линия допускаемого напряжения не пересекает резонансных кривых, резонансные напряжения особой опасности не представляют и режимы п кр2 и п кр3 допустимы для длительной работы. Режим п кр1 опасен для длительной работы, так как прямая допускаемого напряжения отсекает на резонансной кривой участок чрезмерно больших напряжений.
Диапазон частот вращения вблизи п кр1 ( n 1 - n 2 ), называемый критически опасным для длительной работы.
Он является запретной зоной. На циферблатах тахометров запретные зоны частот вращения отмечают красными секторами. Длительная работа в пределах этой зоны недопустима, и переходить ее надо быстро.
Критическую частоту вращения можно установить не только расчетным путем, но и при помощи специального прибора-торсиографа, позволяющего снимать с работающего двигателя графики крутильных колебаний (торсиограммы).
Внешние признаки работы двигателя в зоне критических частот вращения:
сильная вибрация и резкие стуки в двигателе вследствие периодического изменения угловой скорости отдельных кривошипов,
нагрев отдельных участков валопровода (иногда до появления цветов побежалости) вследствие внутреннего трения частиц металла при упругих деформациях кручения.
Если запретная зона частот вращения оказывается в области рабочих режимов двигателя, принимают меры для смещения п кр за пределы этой области. Для этого еще в процессе проектирования установки изменяют частоту свободных колебаний системы путем изменения момента инерции GIp сечения коленчатого вала или валопровода (изменением диаметра вала ), либо моментов инерции θl маховых масс (изменением массы маховика, гребного вала или установкой динамических гасителей колебаний - антивибраторов ), здесь l - расстояние между массами, м.
Иногда прибегают к уменьшению амплитуды резонансных колебаний изменением порядка вспышек в цилиндрах (что не всегда возможно); разделением крутильной системы путем установки между двигателем и валопроводом гидромуфты; установкой специальных гасителей крутильных колебаний - демпферо в (см. рис. 7.16) Общим для всех существующих типов демпферов является наличие между маховой массой и ступицей элемента с трением, поглощающего часть колебательной энергии системы. Сегодня наибольшее распространение находят силиконовые демпферы. Ступица силиконового демпфера (рис. 7.16) жестко крепится к носовому фланцу коленчатого вала, а маховик (свободная масса) размещается внутри корпуса, составляющего одно целое со ступицей. Между поверхностями маховика и корпуса демпфера имеются зазоры в 0,2-0,5 мм, заполняемые силиконовой жидкостью. Энергия крутильных колебаний поглощается трением, возникающим в вязкой среде при относительном движении маховика.
В качестве силиконовой жидкости обычно применяется полиметилсилоксановая жидкость (GVC ). Она обладает рядом ценных свойств: химически инертна, малая зависимость вязкости от температуры (в сравнении с обычными моторными маслами), низкая температура застывания, хорошая смазывающая способность.
 На рис. 7.17 представлен демпфер продольных колебаний, поршень которого жестко связан с валом двигателя, а корпус присоединен к остову двигателя. Полости перед поршнем и за ним заполняются маслом, поступающим под давлением из масляной магистрали. Энергия продольных колебаний гасится на перетекание масла из полостей через дросселирующие отверстия
.
На рис. 7.17 представлен демпфер продольных колебаний, поршень которого жестко связан с валом двигателя, а корпус присоединен к остову двигателя. Полости перед поршнем и за ним заполняются маслом, поступающим под давлением из масляной магистрали. Энергия продольных колебаний гасится на перетекание масла из полостей через дросселирующие отверстия
.
§ 7. 4. Продольные и крутильные колебания вала
Продольные колебания
Этот вид колебаний возникает под действием тангенциальной Т и радиальной Z составляющих сил действия газов и сил инерции масс, нагружающих кривошипы коленчатого вала и вызывающих деформацию колен в виде попеременного расхождения или сближения щек (рис. 7.12). В итоге вал приобретает колебания вдоль оси, которые передаются упорному подшипнику, а через него фундаменту и корпусу судна. Продольные колебания стали особенно заметными с ростом форсирования двигателей, так как увеличилось отношение p z /р е с 7,5 до 10. Продольные колебания возбуждаются также меняющимся упором гребного винта из-за пульсирующего характера действия воды на вращающиеся лопасти и крутильных колебаний валопровода и винта. В целях уменьшения продольных колебаний коленчатого вала и вызываемых ими вибраций судна на носовой фланец вала устанавливают гидравлический демпфер поршневого типа (см. рис. 7.17).
Рис. 7.12. Схема деформациии кривошипа при продольных колебаниях

Колебания в поперечной плоскости
Малооборотный крейцкопфный двигатель, имеющий большую высоту, раскачивается в поперечной плоскости под действием моментов, возникающих в пределах каждого цилиндра от нормальных сил
N
,
передаваемых через крейцкопфный узел параллелям. Частота этих колебаний невелика и равна произведению
п
i
(где
i
- число цилиндров). Для самого двигателя эти колебания неопасны, но они могут вызвать нежелательные высокие местные напряжения в наборе второго дна корпуса судна под фундаментом двигателя. Чтобы этого избежать, остов двигателя в его верхней части раскрепляется с набором корпуса судна в зоне главной палубы с помощью двух пар поперечных связей
1
(рис. 7.13), снабженных эластичным гидравлическим звеном
2.
Наличие этого звена позволяет сохранять постоянной силу натяжения связей вне зависимости от возможных при изменении загрузки судна (плавание в балласте или в грузу) деформаций его корпуса.

§ 7.5. Вибрация корпуса судна
При работе двигателя возникает вибрация как его самого, так и корпуса судна, особенно его кормовой оконечности, трубопроводов, механизмов и пр. Вибрация усиливается при достижении определенной частоты вращения вала двигателя, когда наступает явление резонанса. Резонансные зоны меняются при изменении загрузки судна, мест и способов крепления трубопроводов, механизмов, так как это сказывается на частоте их свободных колебаний. Иногда под действием вибрации в конструкциях образуются трещины.
Источником возмущающих сил являются:
внешне неуравновешенные силы инерции вращающихся и поступательно движущихся масс I и II порядков, под действием которых возникают колебания в горизонтальной и вертикальной плоскостях;
моменты сил инерции центробежных, I и II порядков, стремящиеся опрокинуть двигатель в вертикальной продольной, поперечной и горизонтальной плоскостях, проходящих через его центр тяжести, и вызывающие изгибные колебания корпуса судна в этих плоскостях;
опрокидывающий момент двигателя М опр , действующий в поперечной плоскости и вызывающий колебания в этой плоскости;
силы, вызывающие продольные колебания вала двигателя и создающие в корпусе судна колебания в диаметральной плоскости;
крутильные колебания вследствие неравномерности создаваемого двигателем крутящего момента.
Если структура корпуса судна недостаточно прочная и двигатель работает на оборотах, частота которых совпадает с частотой свободных колебаний самого корпуса, то возникающий резонанс может привести к весьма серьезным последствиям. Единственный способ уйти от резонанса - изменить число оборотов двигателя. В последующем следует искать источник возникающих колебаний и постараться его устранить.
Ослабить вибрацию корпуса судна можно путем локализации колебаний двигателя введением упругой связи между ним и фундаментом. В качестве упругой связи используют резинометаллические или пружинные амортизаторы, устанавливаемые между двигателем и его фундаментом.
Для того чтобы понять сущность действия амортизатора, рассмотрим упрощенную схему (рис. 7.18), в которой двигатель представлен в виде массивного тела массой
m
, закрепленного на пружине жесткостью С. Свободные колебания такой системы будут происходить с частотой


Вынужденные колебания тела вызываются возникающей в нем переменной силой Р, частота изменения которой и соответственно частота вынужденных колебаний v B . Сила Р, будучи неуравновешенной, через пружину частично или полностью передается основанию, возбуждая в нем также колебания. Если обозначить передаваемую силу на нижнем конце пружины через Z , то отношение К = Z / P , называемое коэффициентом передачи, может быть представлено
![]() (7.28)
(7.28)
Из выражения видно, что коэффициент передачи К зависит от соотношения между частотами вынужденных и свободных колебаний тела, но поскольку частота вынужденных колебаний определяется частотой изменения силы и изменить ее нельзя, то для уменьшения коэффициента К остается единственный путь - увеличение отношения v b / v c путем уменьшения частоты свободных колебаний. Последняя, как это следует из формулы (7.27), зависит от жесткости С пружины.
Таким образом, чтобы уменьшить силы, передаваемые двигателем судовому фундаменту, нужно добиться уменьшения коэффициента передачи К путем снижения частоты колебаний v c и соответствующего уменьшения жесткости С амортизатора.
На амортизаторы можно устанавливать лишь двигатели с жестким остовом, в противном случае не исключена деформация фундаментной рамы, являющейся постелью рамовых подшипников. Установка на амортизаторы требует разобщения вала двигателя с валопроводом с помощью гибкой муфты и наличия гибких соединений подходящих к нему трубопроводов, в том числе и выпускного.
K = Z / Р
Из рисунка видно, что если
жесткость пружины

Рис. 7.19. Влияние отношения частот свободных и вынужденных колебаний на коэффициент передачи силы: 1 - без демпфера; 2-с демпфером.
принять бесконечно большой и, тем самым, практически исключить гибкую связь между массой и основанием, то коэффициент передачи будет близок к единице и сила Р будет полностью передаваться основанию. С уменьшением жесткости С коэффициент передачи должен уменьшаться. Однако, в связи с тем, что v B / v c приближается к единице, когда колебания входят в резонанс, амплитуда колебаний резко возрастает, и это влечет за собой увеличение коэффициента передачи практически до бесконечности.Обычно эластичные амортизаторы применяются при установке дизель-генераторов, имеющих общую раму и не требующих разъединения двигателя и генератора с помощью эластичных муфт (рис. 7.20).
Литература
2.Возницкий И. В. Судовые двигатели внутреннего сгорания. Том 2. / И.В.Возницкий, А.С.Пунда – М.:МОРКНИГА, 2010.- 382 с. Стр. 178-188
4.Возницкий И. В. Судовые двигатели внутреннего сгорания. Том 2. / И.В.Возницкий, А.С.Пунда – М.:МОРКНИГА, 2008.- 470 с. Стр. 231-242
5.Возницкий И. В. Судовые дизели и их эксплуатация / И.В.Возницкий, Е.Г.Михеев – М.:Транспорт, 1990. - 360 с. Стр. 272-276
Рассмотрим теперь явление, называемое крутильными колебаниями.
Установка, позволяющая создавать крутильные колебания состоит из штатива с зажимом для закрепления тонкой металлической проволоки, на нижнем конце которой можно подвешивать различные твердые тела (рисю1.4.3). Жестко закрепив концы проволоки в точках Аи В, повернем тело на малый угол вокруг оси проволоки Z и отпустим его. Под действием сил упругости, возникающих при кручении проволоки, тело начнет совершать колебания вокруг оси Z. Их и называют крутильными колебаниями .
Так как это один из видов движения твердого тела вокруг фиксированной оси, то его уравнение движения запишется так (см. лаб. работу № 1.3)
где I – момент инерции подвешенного тела относительно оси проволоки Z, а - момент сил упругости, действующих на тело со стороны проволоки, относительно той же оси. Но в соответствии с уравнением (3) . Тогда, учитывая, что , уравнение (6) можно представить в виде
Это уравнение гармонических колебаний (см. лаб. работу №1.6). Его общее решение можно записать в виде
где - максимальный угол закручивания проволоки (амплитуда колебаний), - начальная фаза колебаний, - циклическая частота колебаний, определяемая формулой
Тогда период крутильных гармонических колебаний
Формулу (10) можно использовать для косвенного измерения как момента инерции тела относительно произвольной оси (ее выбор определяется точкой подвеса тела), так и (с учетом формулы (2)) модуля сдвига материала проволоки.
Измерение момента инерции и модуля сдвига
Момент инерции твердого тела в ряде случаев можно легко рассчитать теоретически. В частности, момент инерции однородного диска (цилиндра), используемого в работе в качестве эталонного тела, относительно оси симметрии Z (рис.1.4.3) задается формулой
где m и D – соответственно масса и диаметр диска.
Подвешивая на одной и той же проволоке эталонное тело с известным , а затем тело с неизвестным моментом инерции I, можно экспериментально определить промежутки времени и , в течение которых совершаются и колебаний эталонным телом и телом с неизвестным моментом инерции. Тогда в соответствии с (10)
Разделив почленно (13) на (12) , после возведения полученного равенства в квадрат находим
В процессе проведения эксперимента целесообразно выбрать . Тогда с учетом (11) для неизвестного момента инерции получаем следующую расчетную формулу
Для измерения модуля сдвига материала проволоки используется только эталонное тело. В этом случае из (11) и (12) с учетом (2) получаем
Порядок выполнения работы
1. Измерить диаметр и длину проволоки.
2. Измерить массу и диаметр эталонного диска.
3. Подвесить к проволоке эталонный диск и измерить время некоторого числа крутильных колебаний (угол закручивания не должен превышать 30°).
4. Подвесить к проволоке за одну из его точек тело с неизвестным моментом инерции (прямоугольная пластина) и измерить время t такого же как для эталонного диска числа колебаний. По формуле (15) рассчитать момент инерции этого тела.
5. Действия по пункту 4 проделать еще раз для двух других точек подвеса (определив таким образом моменты инерции прямоугольной пластины относительно трех взаимно перпендикулярных осей).
6. По известному времени и соответствующему числу колебаний эталонного диска рассчитать по формуле (16) модуль сдвига материала проволоки.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. С какими физическими величинами вы познакомились при изучении теории и в процессе выполнения работы. Дайте определения этих величии.
2. Какие физические законы необходимо знать для понимания настоящей лабораторной работы? Сформулируйте эти законы и объясните, как они применяются в работе.
3. Изобразите графически зависимость от времени , , и проекции момента сил упругости на ось Z.
4. Рассчитайте теоретически моменты инерции ряда тел (диск, цилиндр, шар, конус, прямоугольный параллелепипед относительно разных осей (задача конкретизируется преподавателем)). Сравните полученные результаты с экспериментальными.
5. Получите формулу для расчета момента инерции (15) и формулу для расчета модуля сдвига (16).
6. Справедливо ли следующее утверждение: “Если масса и радиусы шара и диска равны, то момент инерции шара меньше момента инерции диска?”
Литература
1 .Савельев И.В. Курс общей физики - М. Наука, 1988. т.1. - §§ 13,26,28-33.
2. Савельев И.В. Курс общей физики - М. Наука, 1989. т.1. - §§ 38,39,41,43,53.
ЛАБОРАТОРНАЯ РАБОТА №1.5
ИЗМЕРЕНИЕ МОМЕНТА ИНЕРЦИИ МАХОВОГО
КОЛЕСА И СИЛЫ ТРЕНИЯ В ОПОРЕ
Цель работы:
1. Определить момент инерции махового колеса относительно оси вращения.
2. Определить силу трения в опорных стойках оси.
ТЕОРЕТИЧЕСКОЕ ОБОСНОВАНИЕ РАБОТЫ
Моментом инерции твердого тела относительно некоторой оси оо¢ (рис.1.5) называют величину (1) где - масса i – й материальной точки, на которые на которые мысленно разбито тело , R i - ее расстояние до выбранной оси. Если масса сосредоточена в элементарном объеме , а плотность вещества в окрестности рассматриваемой точки тела
То и вместо (1) можно записать
Предлагаемый метод экспериментального определения момента инерции твердого тела основан на изменения механической энергии системы в процессе изучаемого движения (см. лаб.работу 1.2.).
где - кинетическая энергия системы, - ее собственная потенциальная энергия, - суммарная работа всех внешних сил, действующих на систему, - суммарная работа всех внутренних неконсервативных сил.
Если среди внешних сил имеются как консервативные, так и не-консервативные, то суммарная работа консервативных сил, если она не равна тождественно нулю, может быть представлена как убыль некоторой функции координат материальных точек системы , называемой потенциальной энергией системы во внешнем силовом поле. Например, система n – материальных точек, находящихся вне однородного шара массы М, обладает в его гравитационном поле потенциальной энергией вида
где и - соответственно масса i – й материальной точки и ее радиус - вектор, проведенный из центра шара, С - произвольная постоянная. С помощью выражения (4) легко показать, что в пределах небольших высот потенциальная энергия тела массы поверхности Земли равна
где g - ускорение свободного падения у поверхности Земли, h – высота центра инерции тела над произвольно выбранным у поверхности Земли нулевым уровнем потенциальной энергии (это достигается фиксацией в (4) численного значения константы С).
Представляя теперь в виде
где - - убыль потенциальной энергии системы во внешнем поле, - суммарная работа внешних неконсервативных сил, вместо (3) получаем
величину
называют полной механической энергией системы во внешнем поле.
Предлагаемый в данной работе метод определения момента инерции махового колеса основан на использовании закона изменения полной механической энергии системы в поле силы тяжести. В рассматриваемом случае на систему груз + маховик действуют внешние консервативные силы тяжести и реакции опоры, а также неконсервативные силы сопротивления воздуха и трения в опорных стойках махового колеса. Пренебрегая работой силы сопротивления воздуха и работой внутренних неконсервативных сил, пользуясь уравнением (7), запишем
где - работа силы трения в опоре.
Пусть в начальный момент времени подвешенный груз массой m (рис.1.5.2) Находится на высоте h (от наиболее низкого положения, до которого может опустится груз. (рис.1.5.2). Тогда, учитывая возможность произвольного выбора нулевого уровня потенциальной энергии, начальная энергия рассматриваемой системы, в пренебрежении массой нити, будет равна
где П – сумма потенциальной энергии махового колеса со шкивом в поле силы тяжести и собственной потенциальной энергии системы. Считая, что изменение последней в. процессе движения пренебрежимо мало, в нижней точке для полной энергии получаем
Так как, по предположению, движение груза равноускоренное, то в нижней точке
где t – время опускания груза. Поскольку нить сматывается со шкива без проскальзывания, то для угловой скорости в момент t имеем
где r - радиус шкива.
Представляя (15) - (17) в уравнение (12), после преобразований получаем искомую формулу для момента инерции:
Порядок выполнения работы
1. Определить при помощи технических весов массу подвешиваемого груза m.
2. Измерить штангенциркулем радиус шкива r.
3. Намотать на шкив нить с прикрепленным к свободному концу грузом. Установить груз на высоте h 1 . Высоту h 1 отсчитать от наиболее низкого положения, на которое может опускаться груз.
4. По секундомеру определить время движения груза от верхней точки до нижнего положения.
5. Определить высоту h 2 , на которую поднимется груз за счет инерции маховика.
7. Провести измерения для трех различных подвешенных грузов.
8. Вычислить погрешности измерений f и I.
КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Какие физические понятия используются в данной работе? Дайте их определение.
2. Сформулируйте закон изменения полной механической энергии системы во внешнем поле.
3. Какие силы называются консервативными? Эквивалентны ли понятия консервативных и потенциальных сил?
4. Запишите кинематические законы равноускоренного движения материальной точки по прямой и окружности, а также формулу, связывающую линейную и угловую скорости частицы при ее движении по окружности.
5. Получить, пользуясь выражением (4), формулу (5), приняв за нулевой уровень потенциальной энергии поверхность Земли.
6. Обосновать вывод формулы для f и I. сформулировать все необходимые для этого предположения.
Литература
1. Савельев И.В. Курс общей физики. Т.1. – М.: Наука, 1989, §§ 19-22,38,39,41,45,46.
При к-рых упругие элементы испытывают
деформации сдвига. Имеют место в разл. машинах с вращающимися валами: в поршневых
двигателях, турбинах, генераторах, редукторах, трансмиссиях транспортных машин.
К. к. возникают в результате
неравномерности периодич. момента как движущих сил, так и сил сопротивления.
Неравномерность крутящего момента вызывает неравномерность изменения угловой
скорости вала, т. е. то ускорение, то замедление вращения. Обычно вал представляет
собой чередование участков с малой массой и упругой податливостью с более жёсткими
участками, на к-рых закреплены значит. массы. В каждом сечении вала будет своя
степень неравномерности вращения, поскольку в одинаковый промежуток времени
массы проходят разные углы и, следовательно, движутся с разными скоростями,
что создаёт переменное кручение вала и динамич. знакопеременные ,
гл. обр. касательные.
При совпадении частот собств.
колебаний системы с частотой периодич. крутящего момента движущих сил и сил
сопротивления возникают резонансные колебания. В этом случае повышается уровень
динамич. переменных напряжений; возрастает акустич. шум, излучаемый работающей
машиной. Динамич. знакопеременные
напряжения при неправильно выбранных (заниженных) размерах вала, недостаточной
прочности его материала и возникновении могут превысить предел выносливости,
что приведёт к усталости материала вала и его разрушению.
При расчёте К. к. валов
машин часто пользуются расчётной схемой с двумя дисками, соединёнными упругим
стержнем, работающим на кручение. В этом случае собств. частота
где I
1
- 1-го диска, I
2 - момент инерции 2-го диска,
С
-крутильная жёсткость стержня, Для круглого стержня диаметром d
и длиной l С
где G - модуль сдвига. Более сложные расчётные схемы содержат большее число
дисков, соединённых стержнями и образующих последоват. цепи, а иногда - разветвлённые
и кольцевые цепи. Расчёт собств. частот форм и вынужденных К. к. по этим расчётным
схемам производится на ЭВМ.
Др. примером К. к. является
крутильный маятник, к-рый представляет собой диск, закреплённый на одном конце
стержня, работающего на кручение и жёстко заделанного др. концом. Собств. частота
такого маятника![]() где I
- момент инерции диска. Приборы с использованием крутильного маятника
применяют для определения модуля упругости при сдвиге, коэф. внутр. трения твёрдых
материалов при сдвиге, коэф. вязкости жидкости.
где I
- момент инерции диска. Приборы с использованием крутильного маятника
применяют для определения модуля упругости при сдвиге, коэф. внутр. трения твёрдых
материалов при сдвиге, коэф. вязкости жидкости.
К. к. возникают в разнообразных упругих системах; в нек-рых случаях возможны совместные колебания с разл. видами деформации элементов системы, напр. изгибно-крутильные колебания. Так, при определ. условиях полёта под действием аэродинамич. сил иногда возникают самовозбуждающиеся изгибно-крутильные колебания крыла самолёта (т. н. флаттер), к-рые могут вызывать разрушение крыла.
ВСГУТУ. Кафедра «Физика»
№ 3. Определение моментов инерции тел с помощью трифилярного подвеса
Лабораторная работа № 3
Определение моментов инерции тел
с помощью трифилярного подвеса
и проверка теоремы Штейнера
Цель работы
Определение моментов инерции некоторых тел методом крутильных колебаний с помощью трифиллярного подвеса;
Проверка теоремы Штейнера.
Приборы и принадлежности
Трифиллярный подвес, секундомер, линейка, штангенциркуль, исследуемые тела (два диска-груза).
Краткая теория
Одним из методов измерения моментов инерции твердых тел является метод трифиллярного подвеса, совершающего крутильные колебания.
Поэтому, вначале определим, какие колебания называются крутильными, затем ознакомимся с устройством трифиллярного подвеса.
Рис. 1. Крутильные колебания
Гармоническими крутильными колебаниями тела называются периодические движения относительно оси, проходящей через центр масс этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса (рис. 1 ):
где – амплитуда колебаний;
– период колебаний.
Устройство трифиллярного подвеса
Трифиллярный подвес состоит из подвижного диска платформы Р (в дальнейшем просто платформа) массой, радиуса, подвешенного на трех симметрично расположенных нитях (рис 2. a ). Наверху эти нити симметрично закреплены по краям диска Р" меньшего радиуса.
При повороте верхнего диска P" на небольшой угол вокруг вертикальной оси OO" все три нити принимают наклонное положение. Центр тяжести системы несколько приподнимается по оси вращения OO" (рис. 2. b ).

Рис. 2. Трифилярный подвес
Период крутильных колебаний и момент инерции платформы
Пусть при вращении платформа поднимется на высоту, тогда приращение ее потенциальной энергии равно
где – ускорение свободного падения.
При вращении платформы в обратную сторону потенциальная энергия переходит в кинетическую энергию вращательного движения
где – момент инерции платформы;
– ее угловая скорость.
В момент прохождения положения равновесия кинетическая энергия максимальна . Если пренебречь трением, то на основании закона сохранения энергии можно записать для колеблющейся платформы
Угловую скорость платформы можно найти, взяв производную по времени от (см. (1))
Очевидно, что
Найдем величинупри поворотах платформы на угол 0 , считая, что (– длина нити)
![]() (4)
(4)
Из рис. 2 а, b видно, что
![]()
Подставляя значенияив формулу (4) получим
![]()
Ввиду малости угла 0 синус заменим аргументом
Подставляя выражения (3) и (5) в формулу (2), получим окончательно
Поскольку параметры прибора,,во время опыта не меняются, формулу (6) удобно применять в виде
Аддитивность моментов инерции
Аддитивность (лат. additivus – прибавляемый) - свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям.
Например, аддитивность объёма означает, что объём целого тела равен сумме объёмов составляющих его частей. Примеры аддитивных величин: энергия, импульс, энтропия, мощность, давление, электрический заряд.
Общий момент инерции нескольких тел равен сумме моментов инерции отдельных тел, если центр масс каждого из них лежит на оси вращения.
Если на платформу поместить некоторое тело массой, так, чтобы равномерное натяжение нитей не нарушалось, то момент инерцииэтой системы находят по формуле (6) или (7), где вместобудет сумма масс .
А так как момент инерции величина аддитивная , т.е., то можно определить момент инерции исследуемого тела:
где ,– момент инерции платформы и груза.
Теорема Штейнера
Момент инерции телаотносительно произвольной осиAA ’ равен сумме момента инерциитела относительно осиBB ’ , параллельной данной и проходящей через центр масс тела С , и произведения массы телана квадрат расстояниямежду осями (рис. 3 )
В соответствии с теоремой Штейнера момент инерции диска относительно оси AA ’ , равен моменту инерции относительно оси BB ’ , проходящей через центр масс, плюс
Таким образом, с удалением центра масс тела от оси вращения его момент инерции относительно этой оси возрастает. Момент инерции системы тел зависит не только от его массы, но и от распределения масс в системе относительно оси вращения.

Рис. 3. Теорема Штейнера
Ход работы
где – число полных колебаний.
Таблица 1.1
|
Среднее значение | ||||
Таблица 1.2
Таблица 2.1
|
Среднее значение | ||||
Определить момент инерции платформы с грузами в центре по формуле (6).